Cap´ıtulo 2 Formulaç˜ao básica do problema de fluxo de carga 2.1 Motivaç˜ao e idéias gerais

52 Pages·2017·0.25 MB·Portuguese

Cap(cid:19)(cid:16)tulo 2
Formulac(cid:24)~ao b(cid:19)asica do problema de (cid:13)uxo de carga
2.1 Motivac(cid:24)~ao e id(cid:19)eias gerais
I
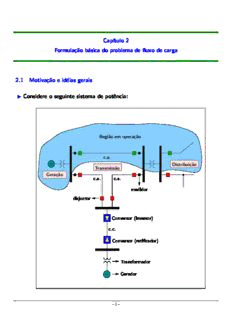
Considere o seguinte sistema de pot^encia:
Regi~ao em operac(cid:24)~ao
c.a.
(cid:24) Distribuic(cid:24)~ao
Transmiss~ao
Gerac(cid:24)~ao
c.a. c.a.
medidor
disjuntor
PSfrag replacements
Conversor (inversor)
c.c.
Conversor (reti(cid:12)cador)
Transformador
(cid:24) Gerador
{ 1 {
I
Considere que:
(cid:4) a func(cid:24)~ao do sistema de gerac(cid:24)~ao (cid:19)e produzir a energia el(cid:19)etrica que ser(cid:19)a
consumida ! modelado como uma injec(cid:24)~ao de pot^encia no barramento
(cid:4) a linha de transmiss~ao (cid:19)e modelada como um circuito RL s(cid:19)erie
(cid:4) o sistema de distribuic(cid:24)~ao consome a energia transportada pelo sistema de
transmiss~ao ! modelado como uma injec(cid:24)~ao de pot^encia no barramento
I
Diagrama uni(cid:12)lar correspondente:
Regi~ao em operac(cid:24)~ao
c.a.
PSfrag replacements
~ Distribuic(cid:24)~ao
Transmiss~ao
Gerac(cid:24)~ao
1 2
r + j x
P + j Q P + j Q
1 1 2 2
P + j Q
12 12
E = V \(cid:18) E = V \(cid:18)
1 1 1 2 2 2
Gerac(cid:24)~ao Transmiss~ao Distribuic(cid:24)~ao
{ 2 {
PSfrag replacements
I
Circuito por fase:
1 r j x 2
I
+ P P +
1 2
(cid:24) E E
1 Q Q 2
1 2
- -
Gerac(cid:24)~ao Transmiss~ao Distribuic(cid:24)~ao
I Dados: S = P + j Q = 100+ j 0 = 100\0(cid:14) MVA (100 MW, 0 Mvar)
2 2 2
V = 500 kV (linha)
2
r = 25 (cid:10)/fase
x = 125 (cid:10)/fase
I
Pede-se: V
1
S = P + j Q
1 1 1
Conhecendo essas grandezas, pode-se dizer que o estado de operac(cid:24)~ao da rede
(cid:19)e totalmente conhecido. A partir da(cid:19)(cid:16) outras an(cid:19)alises podem ser realizadas.
I
Os c(cid:19)alculos ser~ao feitos em pu (por unidade), cuja id(cid:19)eia (cid:19)e muito importante
no caso de circuitos com v(cid:19)arios n(cid:19)(cid:16)veis de tens~ao.
I
Valores de base:
S = 100 MVA V = 500 kV
b b
{ 3 {
Convers~ao dos dados para pu:
S = 1\0(cid:14) pu
2
E = 1\0(cid:14) pu (refer^encia angular)
2
25
r = = 0;01 pu
(V 2=S )
b b
125
x = = 0;05 pu
(V 2=S )
b b
Corrente pelo circuito:
S (cid:3) 1\0(cid:14) (cid:3)
I = 2 = = 1\0(cid:14) pu
E 1\0(cid:14)
2
(cid:18) (cid:19) (cid:18) (cid:19)
Tens~ao na fonte:
E = E + I (r + j x)
1 2
= 1\0(cid:14) + 1\0(cid:14)(0;01 + j 0;05) = 1;0112\2;8(cid:14) pu
Pot^encia fornecida pela fonte:
S = E I(cid:3) = 1;0112\2;8(cid:14) = 1;01 + j 0;05 pu (101 MW, 5 Mvar)
1 1
PSfrag replacements
V = 1;0112 pu V = 1 pu
1 2
1 2
perdas na transmiss~ao
101 MW 100 MW
5 Mvar 0 Mvar
1 MW
5 Mvar
{ 4 {
I
Na pr(cid:19)atica, os dados e inco(cid:19)gnitas n~ao s~ao os especi(cid:12)cados anteriormente.
I Dados: S = P + j Q = 100+ j 0 = 100\0(cid:14) MVA (100 MW, 0 Mvar)
2 2 2
V = 1;0112 pu (*) (linha)
1
r = 25 (cid:10)/fase
x = 125 (cid:10)/fase
(*) Tens~ao na sa(cid:19)(cid:16)da do transformador elevador na subestac(cid:24)~ao da usina,
mantida constante atrav(cid:19)es de um complexo sistema de controle.
I
Pede-se: V
2
S = P + j Q
1 1 1
I
A resoluc(cid:24)~ao anal(cid:19)(cid:16)tica (cid:19)e mais complicada. Pode-se tamb(cid:19)em resolver por
tentativa e erro.
I
Resoluc(cid:24)~ao anal(cid:19)(cid:16)tica
Lei das tenso~es de Kirchho(cid:11):
E = E + ZI
1 2
= E + Z (S =E )(cid:3) ((cid:2)E(cid:3))
2 2 2 2
E E(cid:3) = V 2 + ZS(cid:3)
1 2 2 2
Considerando E = V \0(cid:14) e E = V \(cid:18) :
1 1 2 2 2
V V \ (cid:0) (cid:18) = V 2 + (r + j x)(P (cid:0) j Q )
1 2 2 2 2 2
Separando as partes real e imagin(cid:19)aria:
V V cos(cid:18) = V 2 + (rP + xQ )
1 2 2 2 2 2
V V sen(cid:18) = (rQ (cid:0) xP )
1 2 2 2 2
{ 5 {
Elevando as duas equac(cid:24)o~es ao quadrado e somando-as, elimina-se (cid:18) :
2
V 2V 2 = V 4 + (rP + xQ )2 + 2V 2(rP + xQ ) + (rQ (cid:0) xP )2
1 2 2 2 2 2 2 2 2 2
V 4 + V 2 2(rP + xQ ) (cid:0) V 2 + (rQ (cid:0) xP )2 + (rP + xQ )2 = 0
2 2 2 2 1 2 2 2 2
h i
(cid:2) (cid:3)
que pode ser reescrita como:
V 4 + bV 2 + c = 0 (cid:1) = b2 (cid:0) 4c
2 2
y = (cid:0)b + (cid:1)1=2 =2
1
(cid:16) (cid:17)
y = (cid:0)b (cid:0) (cid:1)1=2 =2
2
(cid:16) (cid:17)
1=2 1=2
V = (cid:6)y ;(cid:6)y
2 1 2
n o
Para os dados fornecidos: V = f(cid:6)1;(cid:6)0;05g pu.
2
A resposta esperada (cid:19)e V = 1 pu. Ent~ao:
2
(cid:18) = sen(cid:0)1[(rQ (cid:0) xP )=V V ] = (cid:0)2;8(cid:14)
2 2 2 1 2
(cid:3)
S
I = 2 = 1\ (cid:0) 2;8(cid:14) pu
E
2
(cid:18) (cid:19)
S = E I(cid:3) = 1;0112\2;8(cid:14) = 1;01 + j 0;05 pu (101 MW, 5 Mvar)
1 1
! Mesma soluc(cid:24)~ao anterior.
{ 6 {
PSfrag replacements
I
Interpretac(cid:24)~ao:
(cid:4) As duas soluc(cid:24)o~es negativas n~ao t^em signi(cid:12)cado f(cid:19)(cid:16)sico ! s~ao desprezadas.
(cid:4) Suponha que a pot^encia ativa da carga no barramento 2 seja vari(cid:19)avel e
que a pot^encia reativa seja nula:
V [pu]
2
operac(cid:24)~ao est(cid:19)avel
1
0,8
caso base V cr
2
0,6
0,1
0,4 Pcr
2
0,2 operac(cid:24)~ao inst(cid:19)avel
0
0 1 2 3 4 5 6 7 8 9
P [pu]
2
Pcr { m(cid:19)aximo carregamento da rede para as condic(cid:24)o~es especi(cid:12)cadas.
2
V cr { tens~ao para a qual ocorre o m(cid:19)aximo carregamento.
2
Exerc(cid:19)(cid:16)cio (1) Apresente a curva [V2 (cid:2)P2] completa para o circuito exemplo, con-
siderando Q2 = 0.
cr cr
(2) Obtenha P e V analiticamente e comparar com os valores obtidos
2 2
atrav(cid:19)es da an(cid:19)alise da curva PV.
(3) Apresente a curva [V2 (cid:2)Q2] considerando P2 = 0 no mesmo gr(cid:19)a(cid:12)co de (1).
cr cr
Obter Q e V analiticamente e comparar com os valores obtidos atrav(cid:19)es
2 2
da an(cid:19)alise da curva PV.
{ 7 {
I
Os sistemas el(cid:19)etricos de pot^encia s~ao din^amicos:
P
2
PSfrag replacementsPcr
2
V cr
2 t
V
2
processo de instabilidade
de tens~ao que resulta no
~
COLAPSO DE TENSAO
t(cid:3) t
! Modelagem dos aspectos din^amicos e m(cid:19)etodos de resoluc(cid:24)~ao espec(cid:19)(cid:16)(cid:12)cos s~ao
necess(cid:19)arios.
I
Para redes maiores:

Resoluc(cid:24)~ao por meios
anal(cid:19)(cid:16)ticos (cid:19)e imposs(cid:19)(cid:16)vel.

Tentativa e erro?
{ 8 {
I
Resoluc(cid:24)~ao por tentativa e erro
Uma id(cid:19)eia de um procedimento de c(cid:19)alculo iterativo:
(a) Inicializar contador de iterac(cid:24)o~es (cid:23) = 0
(b) Escolher E(cid:23) = E0
2 2
(c) Calcular a corrente pela carga:
(cid:3)
S
I(cid:23) = 2
2 E(cid:23)
(cid:18) 2 (cid:19)
(d) Calcular a queda de tens~ao na linha de transmiss~ao:
(cid:1)E(cid:23) = (r + j x) I(cid:23)
2
(e) Calcular a tens~ao na barra de carga:
(cid:3)
S
E(cid:23)+1 = E (cid:0) (cid:1)E(cid:23) = E (cid:0) (r + j x) 2
2 1 1 E(cid:23)
(cid:18) 2 (cid:19)
(f) Incrementar contador de iterac(cid:24)o~es ((cid:23) (cid:23) + 1) e voltar para o passo (c)
Comec(cid:24)ando com E = 1\0(cid:14) pu tem-se:
2
Iterac(cid:24)~ao E [pu]
2
0 1 + j 0
1 1;0012(cid:0) j 0;0500
2 0;9987(cid:0) j 0;0493
3 0;9987(cid:0) j 0;0494
4 0;9987(cid:0) j 0;0494 Soluc(cid:24)~ao: E = 1\ (cid:0) 2;8(cid:14) pu
2
Na realidade este m(cid:19)etodo iterativo (Gauss) foi o primeiro a ser proposto para
a resoluc(cid:24)~ao das equac(cid:24)o~es de (cid:13)uxo de carga ((cid:24) 1956).
{ 9 {
I
Resumo:
(cid:19)
(cid:4) E necess(cid:19)ario o desenvolvimento de t(cid:19)ecnicas de resoluc(cid:24)~ao espec(cid:19)(cid:16)(cid:12)cas e
e(cid:12)cientes para o problema da determinac(cid:24)~ao do estado de operac(cid:24)~ao de
(cid:19)
redes el(cid:19)etricas em regime permanente CALCULO DE FLUXO DE
CARGA
(cid:4) Fluxo de carga (load (cid:13)ow) = Fluxo de pot^encia (power (cid:13)ow)
(cid:19)
(cid:4) E uma ferramenta b(cid:19)asica para a an(cid:19)alise de redes el(cid:19)etricas
2.2 Componentes das redes el(cid:19)etricas
Geradores (G)
Cargas (L) ligados entre um no(cid:19) (barra) qualquer
Reatores shunt (RSh) e o no(cid:19) (barra) terra
I
Capacitores shunt (CSh)
Linhas de transmiss~ao (LT) ligados entre dois no(cid:19)s (barras) quaisquer
Transformadores (TR)
PSfrag replacements
TR
LT
G (cid:24)
CSh L
{ 10 {